Jako sudoku diagram zde chápu standardní diagram, tedy čtverec rozdělený na mřížku 9 x 9 políček či buněk, která tvoří řádky a sloupce o 9 políčcích a jsou dále rozdělena do 9 oblastí 3 x 3 políček, tzv. regionů (dále jen regionů). Sudoku se řídí několika velmi jednoduchými pravidly:
- v každém řádku, sloupci a regionu se musí nacházet celá číselná řada 1 až 9 (na pořadí nezáleží)
- každé z čísel 1 až 9 se může v řádku, sloupci a regionu vyskytovat pouze jednou
- číslo pro prázdné políčko třeba nalézt logickým vyloučením ostatních kandidátů (tj. číslo musí být jedině v tomto políčku a ostatní čísla v něm být nemohou), ne hádáním a metodou pokus omyl
I. Prosté vyloučení
V prvním diagramu je zobrazen pouze holý princip nejzákladnějšího zjišťování políčka s chybějícím číslem. Tento postup lze hojně použít v počátečních fázích řešení jednoduchých diagramů.
Pravidlo Sudoku říká, že v jednom sloupci, řádku nebo regionu musí být právě jeden výskyt čísla od 1 do 9, ne víc, ne míň. V horním regionu 4 ještě není. Zbývají tři políčka, kde by být mohlo. Avšak ve sloupcích se 4 už toto číslo být znovu nemůže! Oba výskyty čísla 4 ve spodním a středním regionu takto vylučují výskyt 4 ve dvou prázdných políčcích horního regionu, zatímco jednoznačně určují jeho výskyt ve zbývajícím třetím políčku (červeně orámované).
Diagram výše je pouze ilustrační, předvyplněných čísel je po celém standardním diagramu více. Toto prosté hledání neprobíhá jen po sloupcích (jako na obrázku výše), ale samozřejmě i po řádcích a dohromady po řádcích a sloupcích, viz následující diagram:
Z diagramu výše je jasně patrno, jak trojitý výskyt čísla 4 (v šedých políčcích) ovlivňuje (určuje), kde jedině může být 4 v levém prostředním regionu, v němž se ještě nevyskytuje. Vzhledem k tomuto regionu jsou ony tři výskyty 4 přítomny ve sloupcích a v řádku, které zasahují do tohoto regionu a nemohou v nich tedy už znovu být, čímž určují, kde 4 být v regionu nemůže. A protože ostatní políčka regionu bývají obsazena jinými čísly (zde konkrétně 7 blokuje druhé možné políčko pro 4), zbývá pouze jediné volné políčko, kde 4 být může a musí (červeně orámované políčko). Poznámka: tento diagram byl generován programem (stupeň easy, počáteční stav).
II. Dopočítávání
Druhým postupem hledání je dopočítávání. Tato metoda je prostá, využívá jak jinak pravidla Sudoku, že totéž číslo může být v jednom řádku, sloupci a regionu pouze jedenkrát.
Pokud si představíte libovolné prázdné políčko v diagramu jako průsečík řádku a sloupce, které se v něm kříží, potom lze spočítat čísla v tomto křížícím se řádku a sloupci (samozřejmě nezapomeňte ani na region, v němž se dané políčko nachází!) a v případě, že chybí pouze jedno číslo v celé řadě 1-9, toto číslo najít. Dopočítávání je velice užitečná metoda, kterou lze použít ve všech druzích obtížnosti (zejména v pozdějších fázích, kdy nejsou již eliminace vidět na první pohled!), protože umožňuje velmi snadno a s jistotou nalézt chybějící číslo, které není na první pohled patrné!
Viz obrázek sám: pokud seřadíte do jedné číselné řady 1-9 všechna čísla vyskytující se v onom šedém "kříži", který má průsečík v červeně orámovaném políčku, jehož číslo hledáte, potom je patrno, že chybí jediné číslo, totiž 7. Toto číslo tedy nutně patří do červeně orámovaného políčka, protože je jasné, že jediné splňuje základní pravidlo Sudoku jediného a právě jednoho výskytu čísla v jednom sloupci, řádku a regionu (proto je šedě obarven také region, v němž se políčko nachází, neboť musíte brát v úvahu i čísla v regionu). Poznámka: tento diagram byl generován počítačovým programem a částečně řešen až do okamžiku, kdy jsem objevil toto konkrétní dopočítávání.
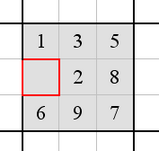Krajně jednoduchým případem dopočítávání je samozřejmě případ jediného chybějícího čísla v regionu. Vyskytuje se buď na začátku nejjednodušších diagramů nebo v pozdějších fázích řešení složitějších. Pokud je v regionu volných více políček, je nutno brát v potaz čísla vyskytující se v těch sloupcích a řádcích, které procházejí tímto regionem a jejichž součástí tato volná políčka jsou...III. Ostře sledovaný sloupec (nebo řádek)
Následující postup je v podstatě opět jednoduchý. Týká se nalezení chybějícího čísla v konkrétním celém sloupci nebo řádku (dále budu psát pouze o sloupci, ale totéž platí v bleděmodrém pro hledání v řádku).
Pokud je ve sloupci už vyplněno (nebo se v něm od začátku nachází) více čísel, je možné pokusit se o nalezení umístění některého z chybějících čísel ve sloupci pomocí řádků, které procházejí prázdnými políčky tohoto sloupce. Samozřejmě vždy také počítejte s celými regiony, kterými prochází daný sloupec! Viz obrázek:
V prostředním sloupci (má celý šedé pozadí) chybí číslo 7. Vyhledáním výskytů čísla 7 v řádcích a regionech, které procházejí prázdnými políčky tohoto sloupce, vyloučíme, kde 7 být nemůže a které jediné políčko zbývá, kde tedy být musí (červeně orámované). Číslo 7 ve středním prostředním regionu vylučuje dvě volná políčka v sloupci (část sloupce je podmnožinou tohoto regionu), číslo 7 v levém spodním regionu vylučuje jedno políčko sloupce (třetí odspodu).
Příklad je poměrně snadný, protože jedno číslo 7 je zde i součástí regionu, jímž sloupec prochází (= eliminuje tak více než jediné políčko sloupce). Někdy je ovšem třeba mezi mnoha čísly velmi pozorně pátrat po celých řádcích, které protínají prázdná políčka daného sloupce (resp. v sloupcích, které protínají prázdná políčka daného řádku). Poznámka: diagram generován programem, počáteční stav.
IV. Vícekrokové eliminace
Název metody popisuje podstatu tohoto postupu: k určení čísla pro prázdné políčko dospějeme až na základě spojení několika předchozích eliminací na jiném místě diagramu. Tyto předchozí eliminace jsou samy pro sebe (= ve svém regionu) sice přibližné, nicméně použity na jiný region, o který nám jde, již plně postačují k logicky nutnému určení chybějícího čísla. Viz obrázek:
Nejprve se podívejte na levý střední region. Podle dvou výskytů čísla 1 (v šedých políčcích) v okolí vidíme, že v tomto regionu může být číslo 1 na dvou možných políčcích (prázdná se šedým pozadím). To nám sice nepomůže pro určení, kde je 1 v tomto regionu, nicméně když se podíváte pozorněji, pochopíte, že právě toto relativně nepřesné určení pozice 1 v tomto regionu přece jen něco sděluje velmi přesně - a totiž fakt, že 1 už je v tomto řádku a v tomto regionu! A tento řádek vede skrze dva další regiony (napravo). A protože v bezprostředně sousedním regionu již číslo 1 je, podíváme se až na region úplně napravo. Nyní vidíme, že oba výskyty 1 v levém a středním regionu jednoznačně určují pozici čísla 1 v tomto krajním pravém regionu (červeně orámované políčko).
Tímto způsobem, totiž několikakrokovou úvahou či eliminací, lze poměrně snadno najít čísla v situaci, kdy již nevidíte eliminace přímo nebo je nelze dopočítat v "kříži" či sloupci / řádku. Výsledkem prvního kroku (úvahy) je zjištění, že určitý řádek nese číslo 1 a že toto číslo je někde v daném regionu. Tím pádem můžeme přistoupit k druhé úvaze pro úplně jiný region, který je však pod vlivem faktu, zjištěného v regionu první úvahy.
Pokud máte chuť, můžete si na obrázku výše najít sami skoro navlas stejnou dvojkrokovou eliminaci opět pro číslo 1. Rozdíl je pouze v tom, že nyní je ve finálním regionu (prostředním horním) číslo 1 nalezeno pomocí celkem tří výskytů 1 (v předchozím případě, který ukazuje obrázek, je totiž region napravo vhodně vyplněn dalšími čísly, tj. 9, 6, 2, takže stačí pouze dva řádky k nalezení hledané pozice, tj. červeného rámečku). Poznámka: diagram generován pro stupeň Hard, počáteční pozice.
Žádné komentáře:
Okomentovat